Die Ermittlung der Rendite (IRR) einer Investition ist mit einigen Fallstricken verbunden. Neben der Auswahl der richtigen Funktion in Excel gibt es einige Dinge zu berücksichtigen, um nicht zu falschen Ergebnissen zu gelangen. Häufig steht man zudem vor der Herausforderung, eine Gesamtrendite für mehrere Projekte oder Investitionen ermitteln zu müssen. Wie dies schnell und flexibel gemacht wird und was dabei zu beachten ist, erläutert dieser Beitrag.
1. Hintergrund
Interner Zinsfuß bzw. IRR
Zur Renditeberechnung von Kapitalanlagen aber auch im Rahmen der dynamischen Investitionsrechnung wird häufig die Interne-Zinsfuß-Methode (auch: Interne-Zinssatz-Methode, Methode des internen Zinsfußes oder Methode des internen Zinssatzes, kurz: IZF -Methode bzw. IZM oder IZS-Methode; englisch: IRR – Internal Rate of Return) verwendet.
Die Methode ermöglicht, für eine Investition oder Kapitalanlage, bei der unregelmäßige und schwankende Erträge anfallen, eine (theoretische) mittlere, jährliche Rendite zu berechnen.
Ein interner Zinsfuß einer Investition ist ein Kalkulationszinssatz, bei dessen Verwendung sich ein Kapitalwert von null ergibt. D.h. der interne Zinsfuß ist der Abzinsungsfaktor, bei dessen Verwendung die diskontierten künftigen Zahlungen dem heutigen Preis/Wert bzw. der Anfangsinvestition entsprechen. Ist dieser Zinsfuß größer als der Kalkulationszinsfuß (d.h. die Rendite ist größer als die Kapitalzinsen plus Risikoaufschlag), ist eine Investition – über die Gesamtlaufzeit berechnet – wirtschaftlich, d.h. vorteilhaft.
Im Folgenden wird erläutert, wie sich mit Excel schnell die IRR einer einzelnen Investitionen bzw. einer Kapitalanlage berechnen lässt und welche Dinge zu beachten sind, um einen „Internen Zinsfuß“ für ein komplettes Investitionsportfolio zu ermitteln. Das Portfolio kann dabei aus beliebig vielen Einzelinvestments mit unterschiedlichen Zeitpunkten und Investitionszeiträumen bestehen.
2. IRR-Ermittlung für Einzelinvestition
Das gewählte einfache Beispiel beinhaltet vier verschiedene Kapitalanlagen/Investitionen für die jeweils die individuelle IRR berechnet werden soll. Schließlich gilt es, die IRR des Gesamtportfolios zu ermitteln.
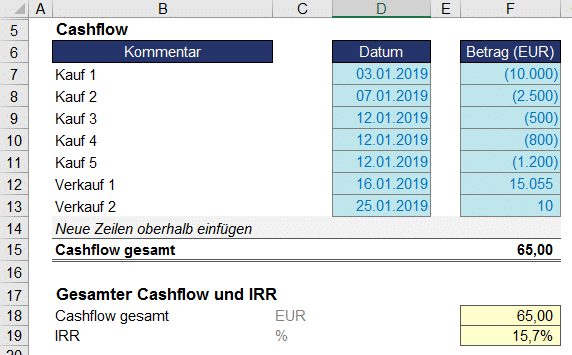
Abb. 1.1 zeigt eine einfache Investition. Alle Auszahlungen sind dabei negativ zu erfassen (Werte in Klammern nach internationaler Konvention negativ), alle Einzahlungen positiv. Excel hält im Grunde zwei verschiedene Funktionen zur Berechnung des Internen Zinsfußes bereit.
Die IKV-Funktion ist die Einfachste. Sie kann allerdings nur für eine Reihe von Zahlungen genutzt werden, die in regelmäßigen Abständen anfallen (z.B. täglich, monatlich, jährlich etc.). In unserem Beispiel haben wir es aber mit unregelmäßigen Zahlungen zu tun, so dass wir die XINTZINSFUSS-Funktion verwenden müssen.
Abb. 1.1: Berechnung der IRR für eine einzelne Investition bzw. Kapitalanlage
Die allgemeine Syntax ist relativ einfach und lautet:
XINTZINSFUSS(Werte; Zeitpkte;[Schätzwert])
Während bei „Werte“ die Aus- bzw. Einzahlungen einzutragen sind, finden sich unter „Zeitpkte“ die zugehörigen Datumswerte der einzelnen Zahlungen. Der Schätzwert ist – erkennbar an den eckigen Klammern – lediglich optional. In den meisten Fällen kann darauf verzichtet werden für die Berechnung von XINTZINSFUSS einen Schätzwert anzugeben. Ist das Argument Schätzwert nicht angegeben, wird es als 0,1 (= 10 Prozent) angenommen.
Wichtig ist, dass die erste Zahlung (im Beispiel in Zelle F7) negativ, also eine Auszahlung sein muss. Dies wird später noch bei der Betrachtung des Gesamtportfolios eine wichtige Rolle spielen.
Für das konkrete Beispiel errechnet sich die IRR also mittels:
=XINTZINSFUSS(F7:F14;D7:D14)
Die beiden Bereiche wurden bewusst um eine Zeile (bis 14) verlängert. Auf diese Weise können später bei Bedarf einfach weitere Zeilen oberhalb von Zeile 14 eingefügt werden und die IRR-Funktion bleibt ohne weitere Eingriffe korrekt.
3. Gesamtrendite eines Investitionsportfolios
Pooled Internal Rate Of Return (= PIRR)
Möchte man die Gesamt-IRR für mehrere Kapitalanlagen berechnen (= Pooled Internal Rate Of Return (PIRR)), kann nicht einfach ein (gewichteter) Durchschnitt der einzelnen Internen-Zinsfüße kalkuliert werden, sondern die einzelnen Cashflows müssen zunächst aggregiert werden. Das heißt, es ist ein neuer saldierter Cashflow (= Gesamt-Cashflow) zu ermitteln. Auf diesen Cashflow kann dann wieder das bereits bekannte Berechnungsverfahren angewendet werden (vgl. Zeile 12 in Abb. 1.2).
 Abb. 1.1: Berechnung der IRR für eine einzelne Investition bzw. Kapitalanlage
Abb. 1.1: Berechnung der IRR für eine einzelne Investition bzw. Kapitalanlage
Schritt 1: Vollständige Zeitleiste
Um die Aggregation automatisch und flexibel zu gestalten, wird zunächst eine übergreifende Zeitleiste benötigt (vgl. Zeile 3). Da im gewählten Beispiel vorher nicht bekannt ist, welche Ein- und Auszahlungsdaten tatsächlich verwendet werden, muss die Zeitleiste auf Tagesbasis angelegt werden und sollte alle Tage berücksichtigten.
Bei längeren Investitionszeiträumen können ggf. viele Spalten erforderlich sein (z.B. bei 5 Jahren 5 x 365 = 1.825 Spalten), die Formeln können aber einfach kopiert werden und seit Excel 2007 stellt auch das Spaltenmaximum keine wirkliche Begrenzung mehr dar (es sind bis zu 16.384 Spalten (A bis XFD) möglich).
Als Alternative bietet sich bei noch längeren Zeiträumen an, die Ein- und Auszahlungsdaten auf Monate zu aggregieren und später für die IRR-Ermittlung das Berechnungsdatum auf die Monatsmitte, also bspw. den 15. Tag, zu setzen.
In der Zeile unterhalb der Tagesdaten werden einfach die einzelnen Tage gezählt (vgl. Zeile 4 in Abb. 1.2). Wir benötigen diese Hilfszeile später zur Verschiebung der Berechnungsbereiche.
Schritt 2: Transformation der Einzel-Cashflows
Hierbei sind zwei Herausforderungen zu meistern. Zum einen sind die Datumswerte und Cashflows bei den Einzelinvestments i.d.R. vertikal, also untereinander, aufgeführt. Zum anderen muss der Cashflow zum richtigen Zeitpunkt eingetragen werden.
Hier können grundsätzlich, wie fast immer in Excel, verschiedene Formeln genutzt werden. Viele Wege führen zum gleichen Ziel. Wir haben uns für die SUMMEWENNS-Funktion entschieden (Achtung „S“ am Ende, nicht verwechseln mit SUMMEWENN).
Deren Syntax lautet:
SUMMEWENNS(Summe_Bereich;Kriterien_Bereich1;Kriterien1;[Kriterien_Bereich2;Kriterien2];…)
Die Funktion funktioniert grundsätzlich ähnlich wie SUMMEWENN, es ist aber unbedingt zu beachten, dass die Reihenfolge der Argumente bei den Funktionen SUMMEWENNS und SUMMEWENN verschieden ist. Das Argument „Summe_Bereich“ ist in SUMMEWENNS das erste Argument, während es in SUMMEWENN das dritte Argument ist.
Für das Projekt Alpha ergibt sich z.B. für Zelle M7:
=SUMMEWENNS(‚Invest 01′!$F$7:$F$11;’Invest 01‘!$D$7:$D$11;‚IRR-Portfolio‘!M$3)*$H7
Durch die gewählte Verriegelung ($-Zeichen) ändert sich im Grunde beim Durchkopieren der Formel durch die gesamte Zeile nur die jeweilige Datumszelle (roter Teil), der Rest bleibt jeweils identisch. Die abschließende Multiplikation mit der Zelle $H7 (in der entweder eine 1 oder eine 0 steht) dient zum Ein- bzw. Ausschalten und wird im Abschnitt Erweiterungsmöglichkeiten weiter unten erläutert.
Prinzipiell ist für diese Operation auch die Verwendung der SUMMEWENN- oder der SUMMENPRODUKT-Funktion möglich. Achtung: Die Verwendung der SVERWEIS-Funktion scheitert, da es mehrere Cashflows mit gleichen Datumswerten gibt. D.h. Datumswerte kommen mehrfach vor, was z.B. bei Aktienportfolios relativ häufig der Fall ist.
Schritt 3: Ermittlung des Gesamt-Cashflow
Die oben für den Cashflow der Investition Alpha aufgeführten Schritte sind für alle Investitionen zu wiederholen (im Bsp. für die 4 Investitionen Alpha bis Delta). Anschließend wird mit einer einfachen Summen-Formel der Gesamt-Cashflow eines jeden Tages aufsummiert (vgl. Zeile 12 in Abb. 1.2).
Schritt 4: Ermittlung IRR Gesamtportfolio
Dies geschieht erneut mittels der XINTZINSFUSS-Funktion. Die Herausforderung besteht hier darin, dass der Bereich „Werte“ zwingend mit einer Auszahlung beginnen muss. Wir können also nicht einfach von Spalte K bis Ende verwenden, sondern im Beispiel darf der Bereich erst in Spalte M (= erste Auszahlung) beginnen.
Dies erreichen wir unter Nutzung der BEREICH.VERSCHIEBEN-Funktion. Allgemein gibt die BEREICH.VERSCHIEBEN-Funktion einen Bezug zurück, der gegenüber einem angegebenen Ausgangsbezug versetzt ist. Der zurückgegebene Bezug kann eine einzelne Zelle oder – wie für unsere IRR-Berechnung benötigt – ein Zellbereich sein. Die Anzahl der zurückzugebenden Zeilen und Spalten kann vorgegeben werden.
Die Syntax lautet:
BEREICH.VERSCHIEBEN(Bezug; Zeilen; Spalten; [Höhe]; [Breite])
Dabei bedeuten die Argumente:
Bezug: Ausgangspunkt des Verschiebevorgangs
Zeilen: Anzahl der Zeilen, um die die obere linke Eckzelle des Bereichs nach oben (= negative Werte) oder nach unten (= positive Werte) verschoben wird.
Spalten: Anzahl der Spalten, um die die obere linke Eckzelle des Bereichs nach links (= negative Werte) oder nach rechts (= positive Werte) verschoben wird.
Höhe: Höhe des neuen Bezugs in Zeilen (pos. nach unten u. neg. nach oben)
Breite: Breite des neuen Bezugs in Spalten (pos. nach rechts u. neg. nach links)
Die beiden letzten Argumente Höhe und Breite sind lediglich optional.
Analysieren wir also die Formel in Zelle F12 mit der die IRR für den Gesamt-Cashflow ermittelt wird. Grundfunktion ist die bereits bekannte XINTZINSFUSS-Funktion mit den beiden Elementen „Werte“ und „Zeitpkte“.
Ziel ist es nun, in einem ersten Schritt den Bereich für „Werte“ so zu definieren, dass dieser automatisch vom ersten negativen Cashflow (im Bsp. Spalte M) bis letzten Datum (im Bsp. Spalte AO) geht.
Wir ermitteln zunächst mittels zwei Hilfszellen, um wie viele Spalten nach rechts verschoben werden muss. Die erste Hilfszelle (hier Zelle D12) liefert das Datum der Spalte in der der erste negative Cashflow steht. Dies wird mittels der folgenden Matrix- bzw. Array-Funktion erreicht: {=MIN(WENN(K12:AO12<>0;K$3:AO$3))}
Diese liefert den kleinsten Datumswert im Bereich K bis AO, sofern die Zellen ungleich Null bzw. leer sind. Die geschweiften Klammern werden nicht mit eingegeben, sondern die Formel wird mit der Tastenkombination [Shift]+[Strg]+[Return] abgeschlossen. Sofern Sie das Thema Matrix- bzw. Arrayformeln vertiefen wollen, empfehlen wir unseren Blogbeitrag „Matrixformeln und deren Verwendung im Financial Modelling“ (siehe: https://fimovi.de/matrixformeln-und-deren-verwendung-im-financial-modelling/).
In der zweiten Hilfszelle (hier Zelle E12) ermitteln wir, dem wievielten Datum/Tag dieses Datum entspricht, d.h. um wieviel wir nach rechtsverschieben müssen. Dies geht mit einer einfachen VERWEIS-Funktion der Form: =VERWEIS(D12;K$3:AO$3;K$4:AO$4)
Jetzt können wir den Bereich für „Werte“ festlegen. Die Formel dazu lautet:
BEREICH.VERSCHIEBEN($K12;0;$E12-1;1;$J$4-$E12+1)
Interpretation: Ausgehend von K12 bleiben wir in der gleichen Zeile (deshalb 2. Argument gleich Null) und müssen um von Spalte K (Ausgangspunkt) nach Spalte M zu kommen, um 2 Spalten verschieben ($E12-1). Die Höhe des Bereiches bleibt eine Zeile (deshalb 4. Argument gleich 1) und die Breite soll bis zum Ende gehen. Da wir insgesamt 31 Spalten haben (aus Max-Funktion in Zelle J4) muss die Breite 29 (=> 31-2) sein, bzw. als allgemeine Formel ($J$4-$E12+1) => 31-3+1=29.
Das gleiche Prinzip wird angewendet, um die korrespondierenden Datumswerte zu erhalten:
BEREICH.VERSCHIEBEN($K$3;0;$E12-1;1;$J$4-$E12+1)
Zusammengesetzt ergibt sich also für die IRR-Formel in Zelle F12:
=XINTZINSFUSS(BEREICH.VERSCHIEBEN($K12;0;$E12-1;1;$J$4-$E12+1);BEREICH.VERSCHIEBEN($K$3;0;$E12-1;1;$J$4-$E12+1))
Achten Sie auf die mit den $-Zeichen vorgenommenen Verankerungen, dann können Sie die Formeln in den Zellen D12, E12 und F12 hoch kopieren und auf diese Weise auch nochmal die IRR-Werte für die Einzelinvestitionen ermitteln und prüfen.
4. Erweiterungsmöglichkeiten
Zwei Ausbau- bzw. Erweiterungsmöglichkeiten bieten sich an. Zum einen wird die Ergänzung von Kontrollzellen empfohlen. Mit diesen kann geprüft werden, ob die hier für die jeweilige Investition ermittelte IRR identisch ist mit dem Berechnungsergebnis auf den Blättern der Einzelinvestitionen. Zum anderen kann noch ein „Schalter“ für jede Investition integriert werden (siehe Spalte H), wodurch später das Portfolio schnell und einfach eingegrenzt werden kann. Dies hilft bspw. im Rahmen von Szenario-Analysen oder falls man sein Portfolio z.B. länder- oder kundenspezifisch auswerten möchte (vgl. Spalten G und H in 1.3).
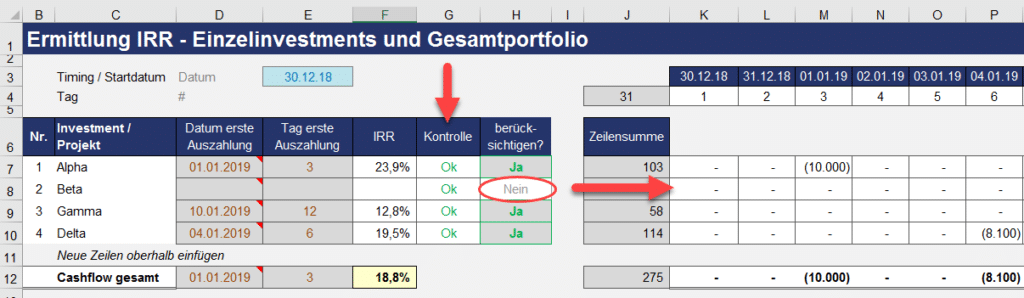 Abb. 1.3: Erweiterungen: Kontrollzellen und AN-/AUS-Schalter
Abb. 1.3: Erweiterungen: Kontrollzellen und AN-/AUS-Schalter
Die Kontrollzelle (z.B. in Zelle G7) zieht einfach den in Zelle F7 ermittelten IRR-Wert von dem auf dem Blatt „Invest 01“ ermittelten ab. Sind beide IRR-Werte identisch, steht in der Zelle eine Null bzw. der Wert „OK“, in allen anderen Fällen erscheint dort eine Fehlermeldung. Falls Sie genauer wissen wollen, wie man derartige Kontrollzellen mit bedingter Formatierung und benutzerdefinierten Zahlenformaten in Excel erstellt, verweisen wir auf unsere Blogbeiträge „Good to Great“ (z.B. unter https://fimovi.de/benutzerdefinierte-zahlenformate-tipps-tricks-zum-intelligenten-formatieren/).
Der EIN-/AUS-Schalter in Spalte G ist nichts weiter als eine 0 (= Aus bzw. Nein) oder eine 1 (= Ein bzw. JA). Die Formel in den Spalten K bis AO zur Transformierung der Cashflow-Werte wird einfach mit der jeweiligen Zelle aus Spalte G multipliziert.
Sofern Sie zu den einzelnen Investitionen weitere Eigenschaften erfassen, z.B. einzelne Länder, können Sie die AN-/AUS-Schalter in Formeln umwandeln und auf diese Weise schnell die Gesamtportfolio-IRR für die eingegrenzten Investments ermitteln (z.B. nur Deutschland, nur USA etc.).
[hr type=“single-line“ style=“solid“ height=“5″ text=“no“][/hr]
[hr type=“without-line“ style=“solid“ height=“5″ text=“no“][/hr]
Wie üblich haben wir auch zu diesem Tutorial eine entsprechende Excel-Datei vorbereitet, die wir ihnen gerne kostenlos zur Verfügung stellen.



2 Antworten
Ich fand den Artikel sehr informativ und hilfreich. Ich habe gelernt, wie man die Rendite (IRR) für ein komplettes Portfolio berechnet, indem man die Cashflows aller Investments zusammenfasst. Das ist eine nützliche Methode, um die Performance des Portfolios zu messen und zu vergleichen. Vielen Dank für den tollen Beitrag!
Vielen Dank für Ihre wertvollen Beiträge sowie die kostenlosen Excel-Dateien!